Vocabulaire
Expérience aléatoire
Une expérience est dite aléatoire lorsque son résultat est lié au hasard et ne peut donc pas être prédit à l'avance avec certitude.
Le lancer d'un dé équilibré à 6 faces constitue une expérience aléatoire : il existe 6 résultats possibles, dont aucun n'est prévisible de façon certaine.
Éventualité
Les résultats possibles d'une expérience sont généralement appelés éventualités (ou issues).
Les éventualités de l'expérience aléatoire consistant à lancer un dé à 6 faces, notées e_i, sont :
- e_1 : face 1
- e_2 : face 2
- e_3 : face 3
- e_4 : face 4
- e_5 : face 5
- e_6 : face 6
Épreuve
On appelle épreuve une expérience dont les différentes issues sont aléatoires et auxquelles on peut attacher des fréquences d'apparition connues ou estimées.
Le lancer d'un dé équilibré à 6 faces constitue une épreuve. On sait que la fréquence d'apparition de chaque face est égale à \dfrac{1}{6}.
Événement
Un événement est un ensemble d'éventualités (ou d'issues).
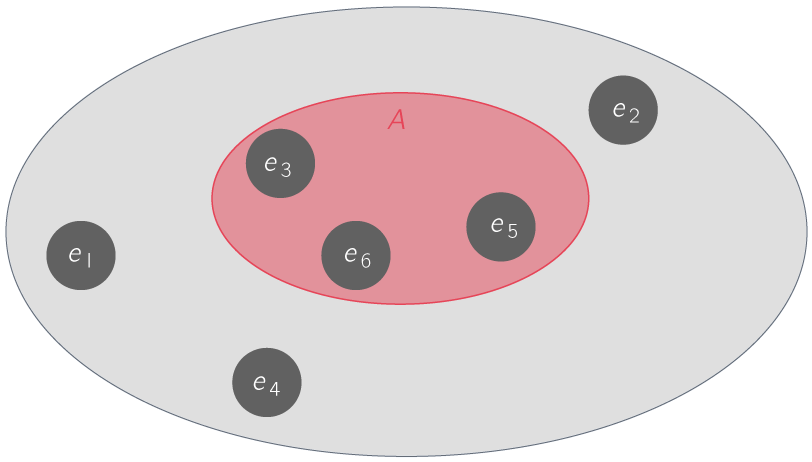
On considère le lancer d'un dé équilibré à 6 faces. On souhaite étudier l'événement A : « obtenir un multiple de 3 ou de 5 ».
Les éventualités correspondant à cet événement sont :
- e_3 : face 3
- e_5 : face 5
- e_6 : face 6
Événement élémentaire
Un événement ne contenant qu'une issue (ou éventualité) est dit élémentaire.
On considère le lancer d'un dé équilibré à 6 faces. On souhaite étudier l'événement A : « obtenir un multiple de 5 ».
L'événement A est un événement élémentaire car il ne contient qu'une issue : « face 5 ».
Événements incompatibles
Deux événements sont dits incompatibles s'ils ne peuvent pas se produire simultanément.
On lance un dé équilibré à six faces. Soient :
- P : « obtenir un nombre pair »
- T : « obtenir 3 »
Les événements P et T sont incompatibles : ils ne peuvent pas se réaliser en même temps.
Événement contraire
On appelle événement contraire de l'événement A, noté \overline{A}, l'ensemble des éventualités qui ne sont pas dans A.
On considère le lancer d'un dé équilibré à six faces. Soit :
M : « obtenir un multiple de 3 » ce qui revient à « obtenir la face 3 ou la face 6 ».
L'événement contraire de M est :
\overline{M} : « ne pas obtenir un multiple de 3 » ce qui revient à « n'obtenir ni la face 3 ni la face 6 ».
Probabilité
Lorsque l'on effectue un très grand nombre de fois une expérience aléatoire de façon indépendante et dans les mêmes conditions, la fréquence de réalisation d'un événement E se rapproche d'un nombre que l'on appelle probabilité de cet événement. On la note p\left(E\right).
La probabilité d'un événement est un nombre compris entre 0 et 1. Elle exprime la « chance » qu'a cet événement de se produire (on dit aussi d'être réalisé).
On peut l'exprimer sous forme d'un nombre à virgule, d'une fraction ou d'un pourcentage.
Événement impossible
Un événement impossible est un événement qui ne peut pas se réaliser. Sa probabilité est 0.
Lorsque l'on lance un dé cubique dont les faces sont numérotées de 1 à 6, l'événement « obtenir 10 » est un événement impossible.
Événement certain
Un événement certain est un événement qui se réalise toujours. Sa probabilité est 1.
Lorsque l'on lance un dé cubique dont les faces sont numérotées de 1 à 6, l'événement « obtenir un nombre inférieur à 10 » est un événement certain.
Si deux événements A et B sont incompatibles, la probabilité qu'au moins un des deux événements se réalise est la somme des probabilités des deux événements. On note :
p\left(A\cup B\right)=p\left(A\right)+p\left(B\right)
On lance un dé cubique dont les faces sont numérotées de 1 à 6. Notons :
- A : « on obtient un nombre pair »
- B : « on obtient un nombre impair »
A et B sont incompatibles, donc p\left(A\cup B\right)=p\left(A\right)+p\left(B\right).
L'événement A\cup B est l'événement « au moins l'un des deux événements A ou B est réalisé ».
Quel que soit l'événement A :
p\left(A\right)+p\left(\overline{A}\right)=1
Autrement dit :
p\left(\overline{A}\right)=1-p\left(A\right)
On lance un dé cubique dont les faces sont numérotées de 1 à 6. On note A l'événement « on obtient un nombre pair ».
Supposons que le dé n'est pas équilibré et que p\left(A\right)=\dfrac{2}{3}.
L'événement contraire de A est \overline{A} : « obtenir un nombre impair ». On a alors :
p\left(\overline{A}\right)=1-p\left(A\right)=1-\dfrac{2}{3}=\dfrac{1}{3}
Cas d'équiprobabilité
Situation équiprobable
On appelle situation équiprobable une expérience où tous les événements élémentaires ont la même probabilité d'être réalisés.
Si on lance un dé équilibré, la probabilité de sortie de chaque face est égale. On est donc dans une situation d'équiprobabilité.
En situation d'équiprobabilité, la probabilité d'un événement A, notée p\left(A\right), est égale à :
p\left(A\right)=\dfrac{\text{Nombre d'éventualités réalisant A}}{\text{Nombre total d'éventualités}}
On lance un dé équilibré à 6 faces. On cherche la probabilité de l'événement A : « obtenir un multiple de 3 ou de 5 ».
Il existe 3 éventualités réalisant cet événement :
- e_3 : face 3
- e_5 : face 5
- e_6 : face 6
De plus, le dé étant équilibré, la situation est équiprobable et chaque face a 1 chance sur 6 de sortir. On en conclut finalement que la probabilité de l'événement A est égale à :
p\left(A\right)=\dfrac{3}{6}=\dfrac{1}{2}
Cas de non équiprobabilité
La probabilité d'un événement est la somme des probabilités des événements élémentaires qui le constituent.
On lance un dé cubique dont les faces sont numérotées de 1 à 6. On suppose le dé non équilibré. Un grand nombre de lancers a permis d'obtenir les résultats suivants :
| Face | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| Probabilité | \dfrac{1}{3} | \dfrac{1}{12} | \dfrac{1}{12} | \dfrac{1}{12} | \dfrac{1}{12} | \dfrac{1}{3} |
Notons A l'événement « obtenir un nombre pair ». On a :
p\left(A\right)=p\left(\left\{ \text{obtenir 2} \right\}\right)+p\left(\left\{ \text{obtenir 4} \right\}\right)+p\left(\left\{ \text{obtenir 6} \right\}\right)
p\left(A\right)=\dfrac{1}{12}+\dfrac{1}{12}+\dfrac{1}{3}
p\left(A\right)=\dfrac{6}{12}=\dfrac{1}{2}
Cette propriété est également valable dans les cas d'équiprobabilité.