Sommaire
IGéométrie planeAAnglesBTrianglesCParallélogrammesDPérimètres et airesIITransformations du plan, agrandissement et réductionASymétriesBAutres transformations du planCTriangles et droites parallèlesIIITrigonométrieGéométrie plane
Angles
Angles opposés par le sommet
Deux angles opposés par le sommet sont de même mesure.

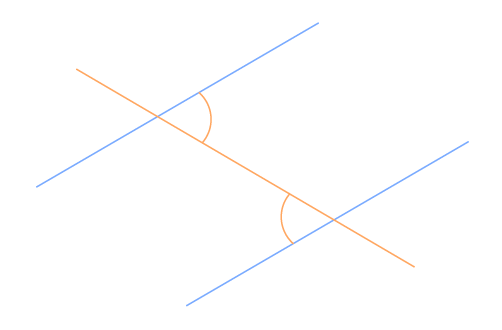
Angles alternes-internes
- Lorsque deux droites parallèles sont coupées par une droite sécante, les angles alternes-internes sont de même mesure.
- Réciproquement, si deux droites coupées par une droite sécante forment deux angles alternes-internes de même mesure, alors elles sont parallèles.
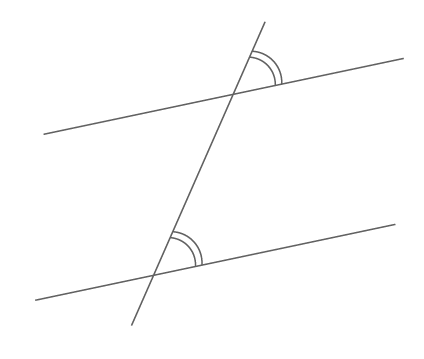
Angles correspondants
- Lorsque deux droites parallèles sont coupées par une droite sécante, les angles correspondants sont de même mesure.
- Réciproquement, si deux droites sont coupées par une même droite et forment deux angles correspondants de même mesure, alors elles sont parallèles.
Triangles
Somme des mesures des angles d'un triangle
La somme des mesures des angles d'un triangle vaut 180°.
Dans le triangle EBC ci-dessous, on cherche à déterminer la mesure de l'angle \widehat{BEC}.
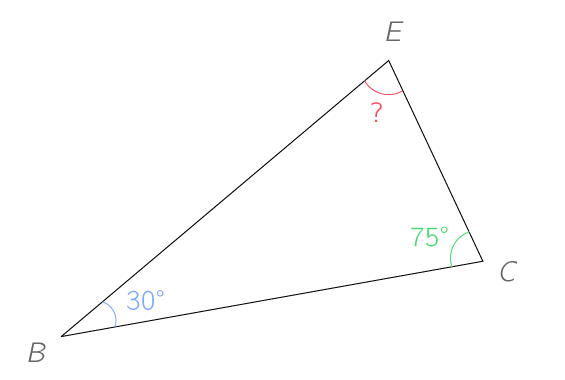
Comme la somme des mesures des angles du triangle EBC vaut 180°, on a :
\widehat{BEC}+\widehat{ECB}+\widehat{CBE}=180
\widehat{BEC}+75+30=180
\widehat{BEC}=180-(75+30)
\widehat{BEC}=75°
Théorème de Pythagore
Dans le triangle ABC rectangle en A, on a :
AB^{2} + AC^{2} = BC^{2}
Le triangle ABC est rectangle en B et vérifie :
AB=5{,}2 cm et AC=6{,}8 cm.

Comme le triangle ABC est rectangle en B, on a, d'après le théorème de Pythagore :
AC^2=AB^2+BC^2
BC^2=AC^2-AB^2
BC^2=6{,}8^2-5{,}2^2
BC^2=19{,}2
BC\approx 4{,}38 cm
Réciproque du théorème de Pythagore
Si dans un triangle ABC, l'égalité BC^2=AB^2+AC^2 est vérifiée alors le triangle ABC est rectangle en A et \left[ BC \right] est l'hypoténuse du triangle.
Le triangle EFG est tel que EF=4{,}5 cm, FG=6 cm et EG=7{,}5 cm.
Alors,
- EF^2+FG^2=4{,}5^2+6^2=56{,}25
- EG^2=7{,}5^2=56{,}25
Ainsi, EF^2+FG^2=EG^2.
D'après la réciproque du théorème de Pythagore, le triangle EFG est rectangle en F et [EG] est l'hypoténuse de ce triangle rectangle.
Parallélogrammes
Caractérisation d'un parallélogramme
| Si un quadrilatère convexe (c'est-à-dire non croisé) a : | Ses côtés opposés parallèles deux à deux | Alors, ce quadrilatère est un parallélogramme. |
| Ses côtés opposés deux à deux de même longueur | ||
| Deux côtés parallèles et de même longueur | ||
| Ses diagonales qui se coupent en leur milieu |
Caractérisation d'un losange à partir d'un parallélogramme
| Si un parallélogramme a : | Deux côtés consécutifs de même longueur | Alors, ce parallélogramme est un losange. |
| Ses diagonales qui sont perpendiculaires |
Caractérisation d'un rectangle à partir d'un parallélogramme
| Si un parallélogramme a : | Un de ses angles droit | Alors, ce parallélogramme est un rectangle. |
| Ses diagonales qui sont de même longueur |
Périmètres et aires

Transformations du plan, agrandissement et réduction
Symétries
Symétrie axiale
Le point M' est le symétrique du point M par la symétrie orthogonale d'axe \Delta si la droite \Delta est la médiatrice du segment [MM'].
Le point S est le symétrique du point P par rapport à la droite \left( d \right).

Symétrie centrale
Le point M' est le symétrique du point M par la symétrie centrale de centre O si le point O est le milieu du segment [MM'].
Le point A' est le symétrique du point A par rapport au point O.

La symétrie centrale transforme :
- Une droite en une droite parallèle à la première
- Un segment en un segment parallèle au premier
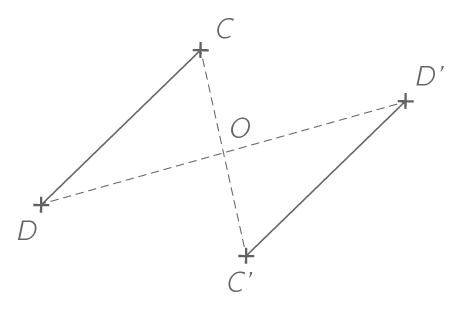
Le segment [C'D'] est le symétrique du segment [CD] par rapport au point O.
On a donc \left(C'D'\right)//(CD).
Les symétries axiales et centrales conservent l'alignement, les longueurs, le parallélisme, les mesures d'angles et les aires.
Le segment [C'D'] est le symétrique du segment [CD] par rapport au point O.
On a donc C'D'=CD.
Autres transformations du plan
Rotation
- Transformer une figure par rotation revient à la faire pivoter d'un angle donné autour d'un point, son centre. Le sens inverse des aiguilles d'une montre est appelé sens direct.
- Dans le sens direct, le point A' est l'image du point A par la rotation de centre O et d'angle \alpha : lorsque OA=OA', l'angle \widehat{AOA'} mesure \alpha ° et on tourne de A vers A' dans le sens direct.
Le point A' est l'image du point A par la rotation de centre O et d'angle \alpha=70°.

Translation
Transformer une figure par translation revient la faire glisser d'une longueur donnée, le long d'une droite donnée et dans un sens donné.
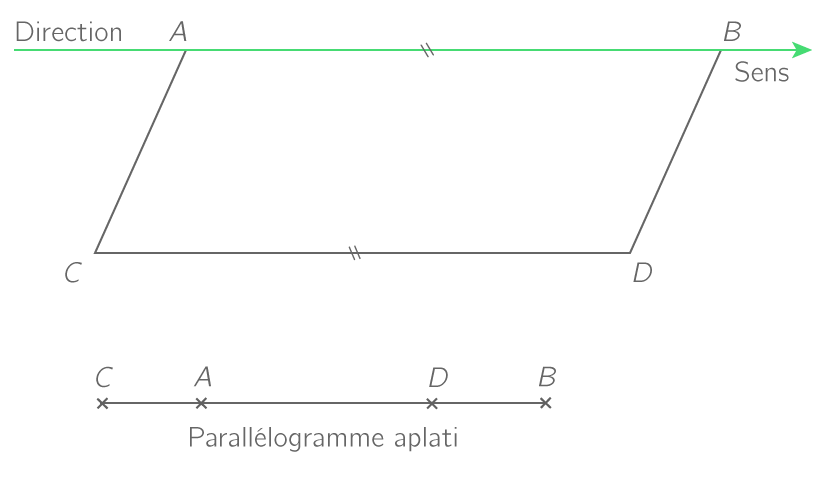
Si la translation qui transforme A en B transforme aussi C en D, alors ABDC est un parallélogramme éventuellement aplati.
Les translations et les rotations conservent l'alignement, les longueurs, les mesures d'angle, le parallélisme et les aires

Homothétie
M' est l'image de M par l'homothétie de centre O et de rapport k
(k un nombre réel différent de 0) lorsque :
- Si k est positif : M'\in [OM) ou si k est négatif : O \in [MM']
- OM' = k OM si k est positif, OM' = – k OM si k est négatif

Par une homothétie de rapport k (k étant un nombre réel), l'image
- D'une droite est une droite qui lui est parallèle.
- D'un segment [MN] est un segment [M'N'] de longueur k MN (si k > 0) ou –k MN (si k < 0).
Le carré A'B'C'D' est l'image du carré ABCD par l'homothétie de centre O et de rapport -0{,}5.

Si une figure \mathcal{F}' est l'image d'une figure \mathcal{F} par une homothétie de rapport k\neq 0, alors :
- Si k<-1 ou k>1, \mathcal{F}' est un agrandissement de \mathcal{F} de rapport -k (si k<-1) ou k si k>1.
- Si -1<k<1, \mathcal{F}' est une réduction de \mathcal{F} de rapport -k (si k<0) ou k si k>0.
Dans l'exemple précédent, le carré A'B'C'D' est une réduction du carré ABCD de rapport \dfrac{1}{2}.
Triangles et droites parallèles
Théorème de Thalès
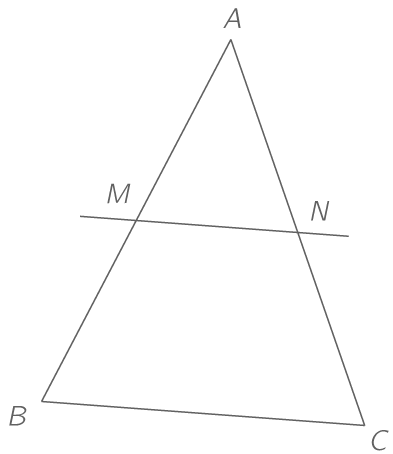
Soit un triangle ABC et soient deux points M et N respectivement sur les droites (AB) et (MN).
Si (MN) et (BC) sont parallèles, alors :
\dfrac{AM}{AB}=\dfrac{AN}{AC}=\dfrac{MN}{BC}

Réciproque du théorème de Thalès
Soient cinq points A, B, C, M et N. Si,
- M\in (AB)
- N\in (AC)
- A, M et B sont alignés dans le même ordre que A, N et C
- \dfrac{AM}{AB}=\dfrac{AN}{AC} ou \dfrac{AM}{AB}=\dfrac{MN}{BC} ou \dfrac{AN}{AC}=\dfrac{MN}{BC}
Alors, les droites \left( MN \right) et \left( BC \right) sont parallèles.
On considère la configuration suivante dans laquelle :
- H, M et A sont alignés
- L, M et T sont alignés
- HM=4 cm, MA=3, LM=6 cm et MT=8 cm
On a donc :
- A\in (HM)
- L\in (MT)
- H, M et A sont alignés dans le même sens que L, M et T
- \dfrac{ML}{MT}=\dfrac{6}{8}=\dfrac{3}{4} et \dfrac{MA}{MH}=\dfrac{3}{4}=\dfrac{ML}{MT}
D'après la réciproque du théorème de Thalès, les droites \left( HT \right) et \left( LA \right) sont donc parallèles.

Proportionnalité des longueurs et des aires
Avec les mêmes notations que pour le théorème de Thalès, posons
k =\dfrac{AM}{AB}
Les relations suivantes sont alors vérifiées :
- AM = k \times AB
- AN = k \times AC
- MN = k \times BC
- \mathcal{A}ire\left(AMN\right) = k^{2} \times \mathcal{A}ire\left(ABC\right)
Avec les notations précédentes,
Si k \gt 1, le triangle AMN est un agrandissement du triangle ABC.
Si k \lt 1, le triangle AMN est une réduction du triangle ABC.
Trigonométrie
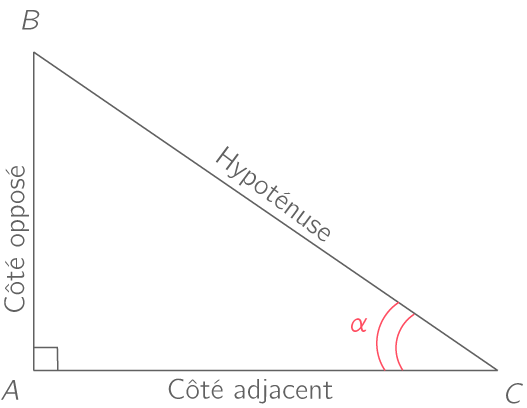
Trigonométrie dans un triangle rectangle
On considère un triangle ABC rectangle en A.
On note \alpha l'angle \widehat{ABC}.
Alors, on définit :
| Cosinus | Sinus | Tangente |
| \cos(\alpha)=\dfrac{\text{côté adjacent}}{\text{hypoténuse}} | \sin(\alpha)=\dfrac{\text{côté opposé}}{\text{hypoténuse}} | \tan(\alpha)=\dfrac{\text{côté opposé}}{\text{côté adjacent}} |
| \cos\left(\widehat{ABC}\right)=\dfrac{AB}{BC} | \sin\left(\widehat{ABC}\right)=\dfrac{AC}{BC} | \tan\left(\widehat{ABC}\right)=\dfrac{AC}{AB} |

On peut se servir de la trigonométrie dans un triangle rectangle pour calculer des longueurs de côtés ou des valeurs approchées de mesures d'angles.
On considère le triangle suivant :
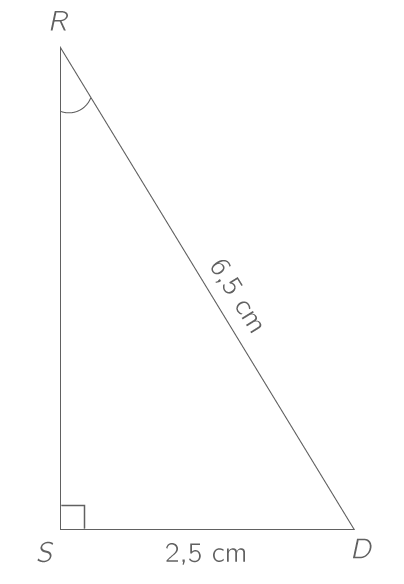
On a donc :
\sin\left(\widehat{SRD}\right)=\dfrac{SD}{RD}
\sin\left(\widehat{SRD}\right)=\dfrac{2{,}5}{6{,}5}
\sin\left(\widehat{SRD}\right)=\dfrac{5}{13}
En utilisant la touche \sin^{-1} (ou arcsin) de la calculatrice, on obtient :
\widehat{SRD}\approx 22{,}6°
Avec les notations de la définition précédente, on a :
| Relations trigonométriques fondamentales |
| \cos^2\left(\alpha\right)+\sin^2\left(\alpha\right)=1 |
| Pour tout angle aigu \alpha différent de 90° : \tan\left(\alpha\right)=\dfrac{\sin\left(\alpha\right)}{\cos\left(\alpha\right)} |
Attention, si la position de l'angle \alpha change, les côtés, adjacent et opposé, sont inversés.