Sommaire
ILes solides de référenceALa perspective cavalièreBLe parallélépipède rectangle et le cubeCLa pyramide et le tétraèdreDLe cylindre de révolutionELe cône de révolutionFLa sphère et la bouleIICaractérisation des droites et plans de l'espaceALes droites de l'espaceBLes plans de l'espaceIIILes positions relatives dans l'espaceALa position relative de deux droitesBLa position relative d'une droite et d'un planCLa position relative de deux plansDPlans parallèles et droites parallèlesLes solides de référence
La perspective cavalière
Perspective cavalière
La perspective cavalière ou parallèle est une forme de représentation des solides. Elle a la particularité de conserver le parallélisme.
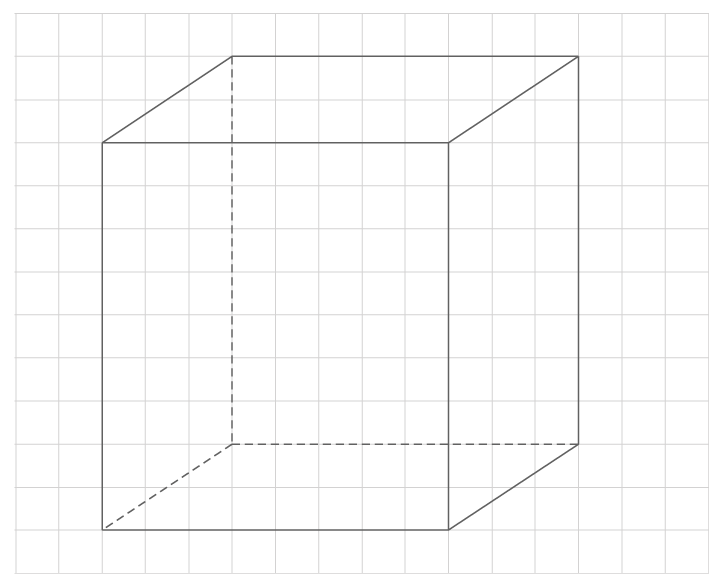
En perspective cavalière, trois points alignés sont représentés par trois points alignés.
Attention, la réciproque est fausse.

Les points A, B et C semblent alignés mais ce n'est pas le cas. Ils sont situés sur 3 arêtes distinctes.
En perspective cavalière, le milieu d'un segment est représenté par le milieu du segment dessiné.
En perspective cavalière, les arêtes visibles sont représentées en trait plein et celles qui sont invisibles en pointillés.
En perspective cavalière, dans un plan de face, des droites perpendiculaires sont représentées par des droites perpendiculaires. Pour les plans qui ne sont pas de face, cela n'est pas respecté.
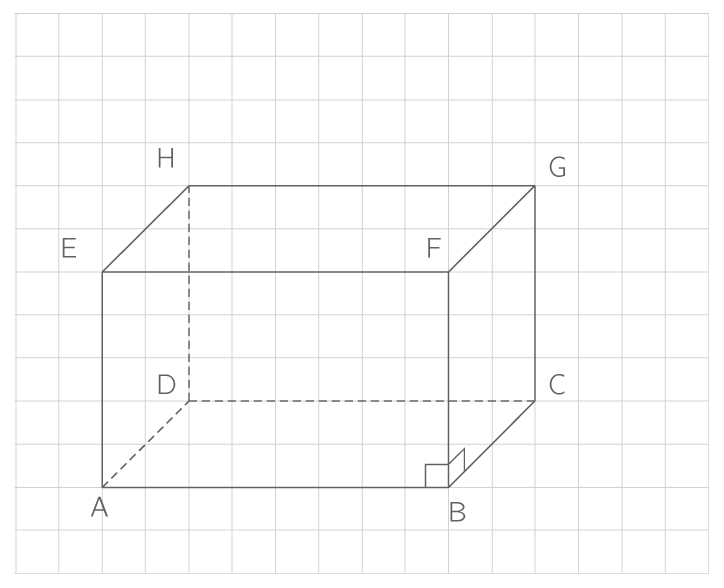
Dans le parallélépipède rectangle ABCDEFGH, on a (AB) \perp (BF) et (BC) \perp (BF).
Cependant, sur le dessin en perspective, les droites (AB) et (BF) apparaissent bien perpendiculaires, car elles sont dans un plan de face, alors que les droites (BC) et (BF) ne semblent pas orthogonales.
Le parallélépipède rectangle et le cube
Parallélépipède rectangle
Un parallélépipède rectangle (ou pavé droit) est un solide à six faces dont toutes les faces sont des rectangles.
Les faces opposées d'un parallélépipède rectangle sont parallèles.
Volume d'un parallélépipède
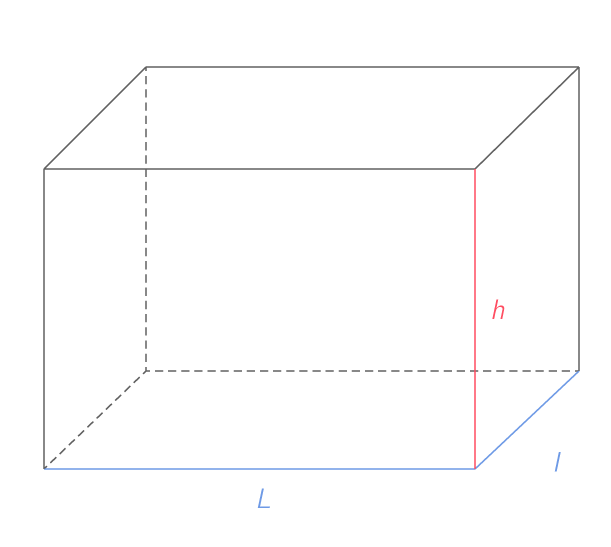
Le volume V d'un parallélépipède rectangle est égal à :
V = L \times l \times h
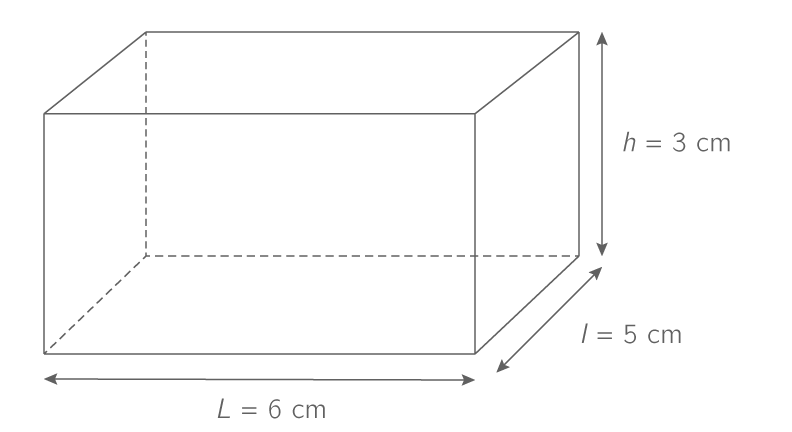
Le volume de ce parallélépipède rectangle est égal à :
V=6 \times 5 \times 3 = 90 cm3
Dans la formule du volume du parallélépipède rectangle, les trois distances doivent être exprimées dans la même unité.

Un cube est un parallélépipède dont les faces sont des carrés.
La pyramide et le tétraèdre
Pyramide
On définit une pyramide à partir d'une base polygonale d'aire B et d'un sommet S. Soit H le projeté orthogonal de S sur la base, on appelle hauteur h de la pyramide la longueur SH.

Dans une pyramide, toutes les faces autres que la base sont des triangles.
Volume d'une pyramide
Le volume V d'une pyramide est égal à :
V =\dfrac{1}{3}\times h \times B
Où h est la hauteur de la pyramide et B l'aire de la base correspondante.

La pyramide à base carrée ci-dessus a pour volume :
V=\dfrac13\times7\times\left(6\times6\right)=84 cm3
Tétraèdre
Un tétraèdre est une pyramide dont la base est un triangle.
Le cylindre de révolution
Cylindre de révolution
On définit un cylindre de révolution à partir de deux bases circulaires parallèles de rayon R, telles que le projeté orthogonal du centre d'une base sur l'autre soit également le centre de la base sur laquelle on projette. On appelle hauteur du cylindre de révolution la distance entre les centres des deux bases et on la note h.

Volume d'un cylindre de révolution
Le volume V d'un cylindre de révolution est égal à :
V = h \times \pi R^{2}
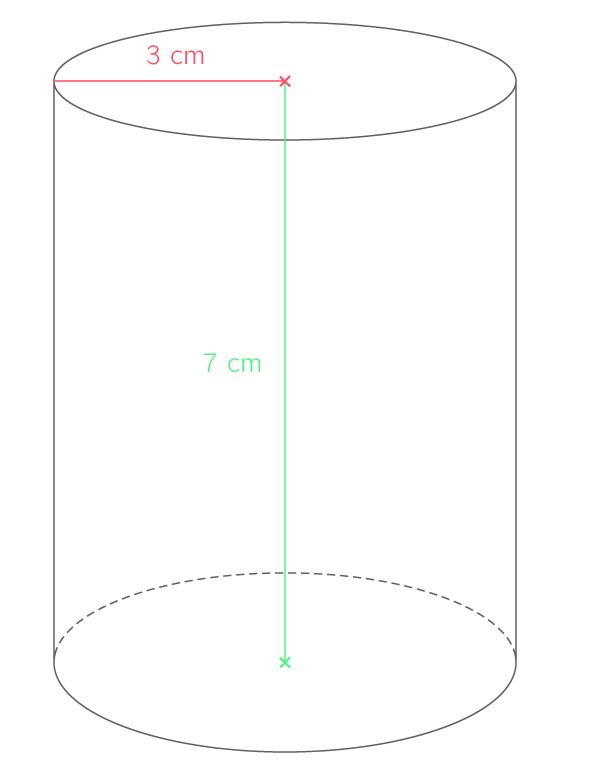
Le volume V du cylindre de révolution ci-dessus est égal à :
V=\pi \times 3^2 \times 7 = \pi \times 9 \times 7 = 63\pi cm3
Le cône de révolution
Cône de révolution
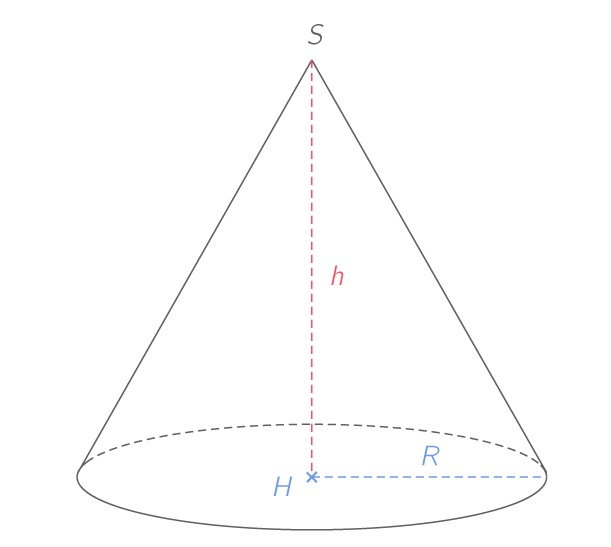
On définit un cône de révolution à partir d'un disque de rayon R et d'un sommet S, tel que le projeté orthogonal H de S sur le disque de base soit le centre de ce disque. On appelle hauteur du cône la longueur SH et on la note h.
Volume d'un cône
Le volume V d'un cône de révolution est égal à :
V =\dfrac{1}{3}\times h \times \pi R^{2}
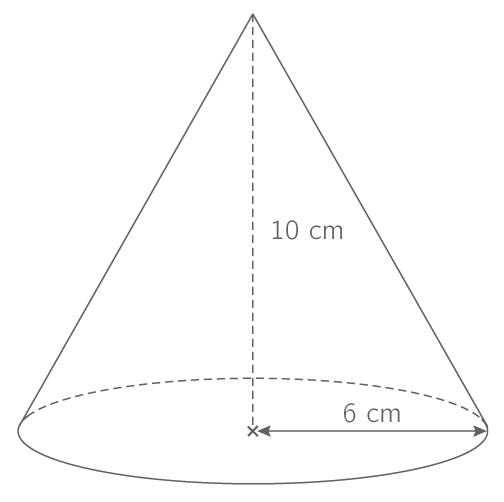
Le volume du cône ci-dessus est :
V=\dfrac13\times10\times\pi\times6^2=120\pi cm3
Soit :
V\approx377 cm3
La sphère et la boule
Boule
La boule de centre O et de rayon R est définie comme l'ensemble des points de l'espace situés à une distance inférieure ou égale à R du point O.

Sphère
La sphère de centre O et de rayon R est l'ensemble des points de l'espace situés à une distance R du point O.
Volume d'une boule
Le volume V d'une boule de rayon R est égal à :
V =\dfrac{4}{3}\times \pi R^{3}
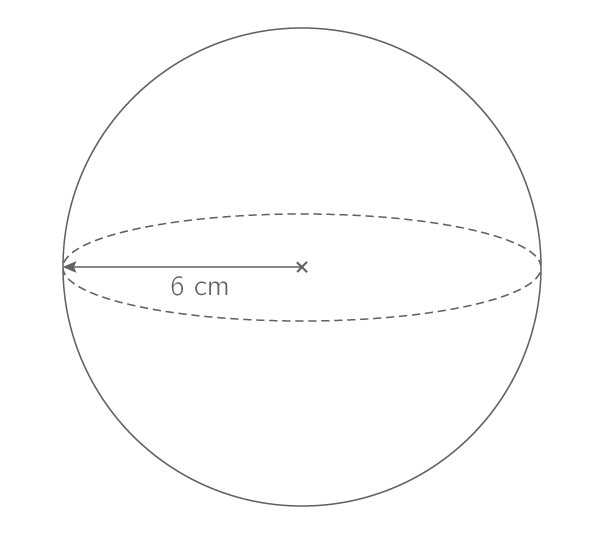
Le volume de la boule ci-dessus est :
V=\dfrac43\times\pi\times6^3=\dfrac{864}{3}\pi=288\pi cm3
Aire d'une sphère
L'aire A d'une sphère de rayon R est donnée par la formule suivante :
A=4\pi R^2
L'aire d'une sphère de rayon 6 cm est :
A=4\times\pi\times 6^2=144\pi\approx452{,}16 cm2
Caractérisation des droites et plans de l'espace
Les droites de l'espace
Droite
Une droite est définie par deux points distincts.

Sur le schéma ci-dessus, les points A et B définissent une droite notée \left( AB \right).
Les plans de l'espace
Plan
Un plan est défini par trois points non alignés.
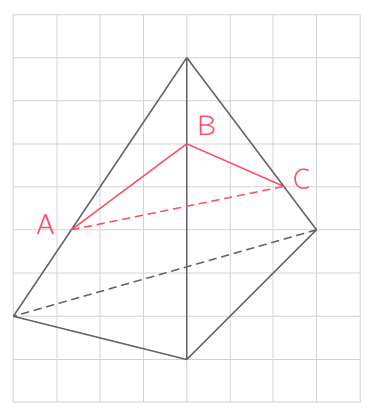
Les trois points A, B et C définissent un plan que l'on note (ABC).
Les positions relatives dans l'espace
La position relative de deux droites
Deux droites de l'espace peuvent être coplanaires si elles sont contenues dans le même plan, ou non coplanaires dans le cas contraire.
L'intersection de deux droites non coplanaires est vide.
Deux droites coplanaires de l'espace peuvent être sécantes en un point ou parallèles.

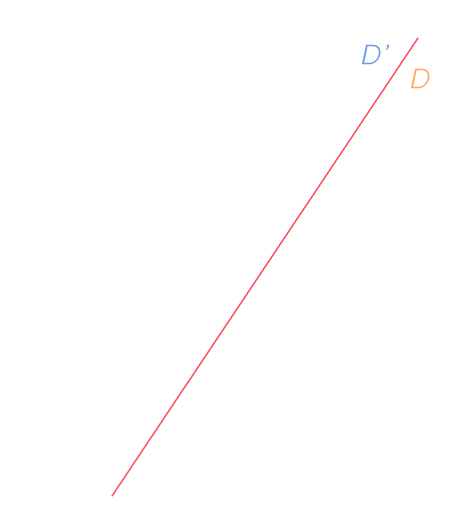
Deux droites parallèles de l'espace peuvent être strictement parallèles ou confondues.
L'intersection de deux droites confondues est une droite.
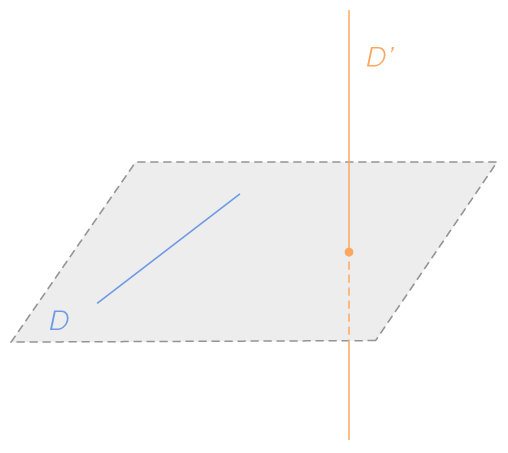
La position relative d'une droite et d'un plan
Une droite peut être contenue dans un plan, sécante avec le plan ou strictement parallèle au plan.
L'intersection d'un plan (P) avec une droite (D) strictement parallèle à (P) est vide.
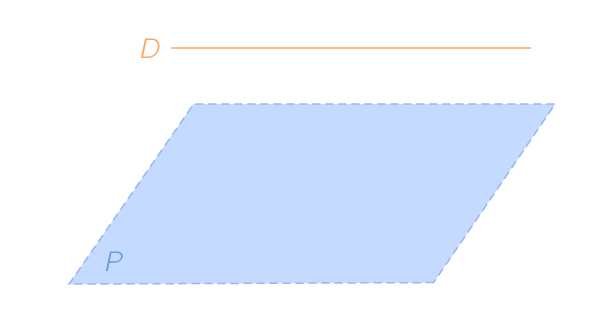
L'intersection d'une droite (D) contenue dans un plan (P), avec ce plan (P) est la droite (D).

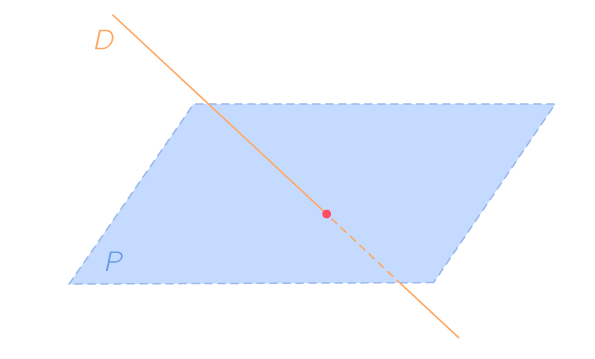
L'intersection d'un plan (P) avec une droite (D) sécante est un point.
La position relative de deux plans
Deux plans peuvent être sécants, parallèles (strictement ou confondus).
Si deux plans sont parallèles alors ils sont soit strictement parallèles, soit confondus.
L'intersection de deux plans confondus est un plan.

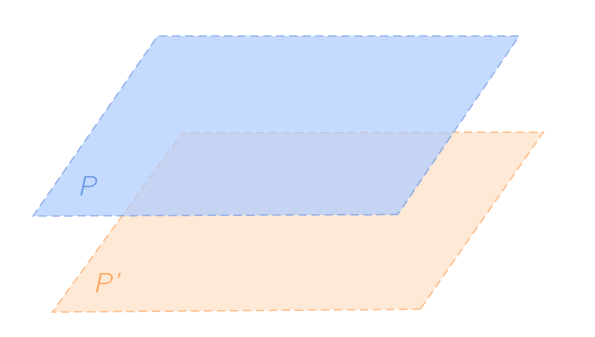
L'intersection de deux plans strictement parallèles est vide.
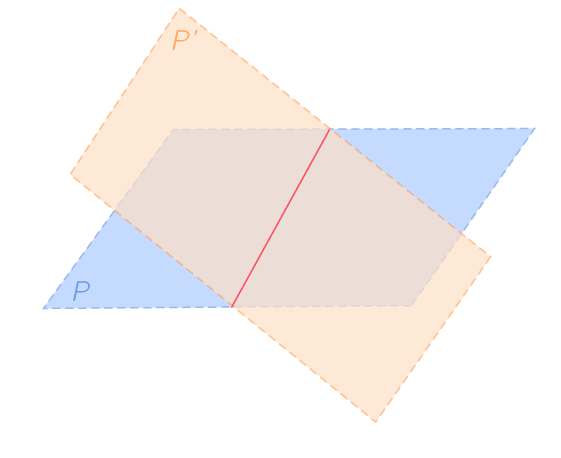
L'intersection de deux plans sécants est une droite.
Plans parallèles et droites parallèles
Plans et droites parallèles
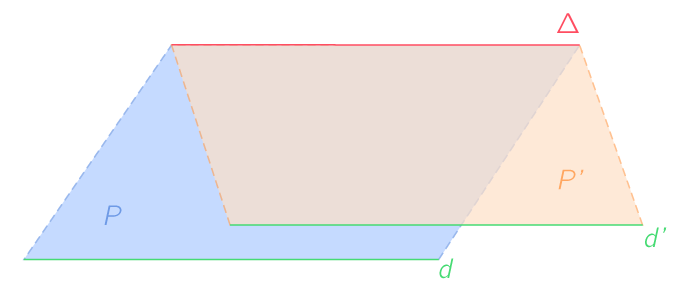
Si un plan coupe deux plans parallèles, alors les droites d'intersection sont parallèles.

Théorème du toit
Soient deux plans P et P' ayant pour intersection la droite \Delta . Si (d) appartenant à P et (d') appartenant à P' sont parallèles, alors ces deux droites sont également parallèles à \Delta .