ABCD est un rectangle tel que AB=12 cm et AD=8 cm.
Soit EFGH le quadrilatère tel que :
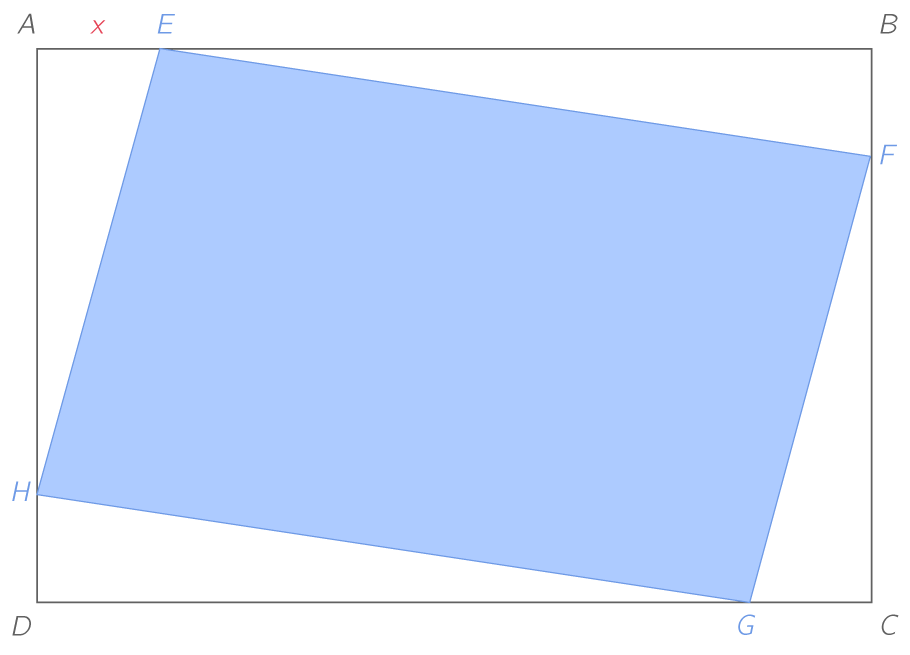
- Les points E, F, G et H appartiennent aux segments \left[AB\right], \left[BC \right], \left[CD \right] et \left[ DA\right]
- AE=BF=CG=DH=x
On appelle f la fonction qui associe à x l'aire du quadrilatère EFGH.
Quelles sont les valeurs possibles de x ?
Quelle est l'expression de la fonction f qui associe à x l'aire du quadrilatère EFGH ?
La forme canonique de f(x) est : f\left(x\right)=2\left(x-5\right)^{2}+46.
Quelle est la valeur de x pour laquelle l'aire d'EFHG est minimale ? Que vaut cette aire minimale ?