Sommaire
IGénéralitésASymétrique d'une figureBLes propriétés de la symétrie axialeIILes axes de symétrie d'une figureACas généralBLa médiatrice d'un segmentGénéralités
Symétrique d'une figure
Symétrie axiale
Deux figures sont symétriques par rapport à une droite \left( d \right) si elles sont superposables par pliage le long de cette droite. On parle alors de symétrie axiale (ou orthogonale), d'axe \left( d \right) et la droite \left( d \right) est appelée axe de symétrie.
Ces deux figures sont symétriques par rapport à la droite \left( d \right).

Les propriétés de la symétrie axiale
En particulier, dans le cadre d'une symétrie axiale :
- Le symétrique d'un segment est un segment de même longueur.
- Le symétrique d'une demi-droite est une demi-droite.
- Le symétrique d'une droite est une droite.
- Le symétrique d'un angle est un angle de même mesure.
- Le symétrique d'un cercle est un cercle de même rayon.
- Les symétriques de trois points alignés sont trois points alignés.
On dit que la symétrie axiale conserve les longueurs, les angles, les aires et l'alignement.

Les axes de symétrie d'une figure
Cas général
Axe de symétrie
La droite \left( d \right) est un axe de symétrie d'une figure si les deux parties de cette figure se superposent par pliage le long de la droite.
La droite \left( d \right) est un axe de symétrie de la figure.

La figure 1, qui est un carré, possède 4 axes de symétrie. La figure 2, quelconque, n'en a pas.

Les axes de symétrie des figures usuelles sont les suivants :

La médiatrice d'un segment
Médiatrice d'un segment
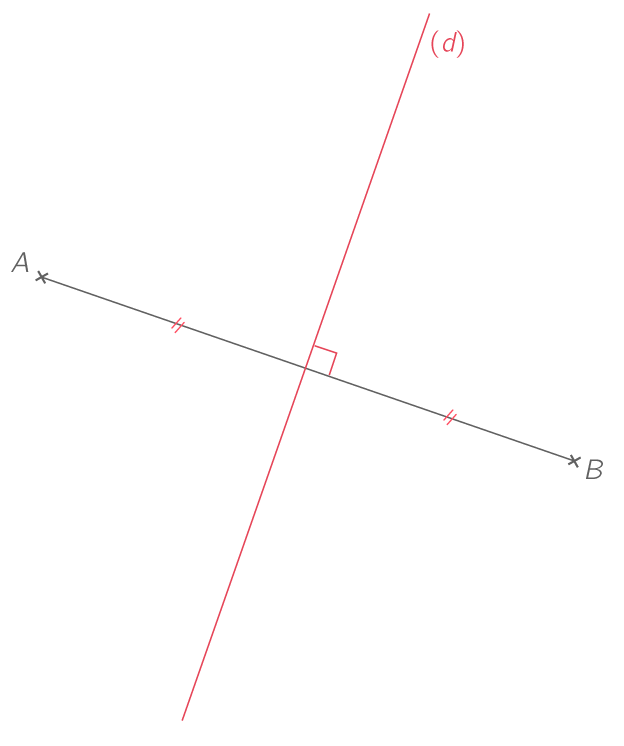
La médiatrice d'un segment est la droite perpendiculaire à ce segment qui passe par son milieu.
La droite \left( d \right) est la médiatrice du segment \left[ AB \right].
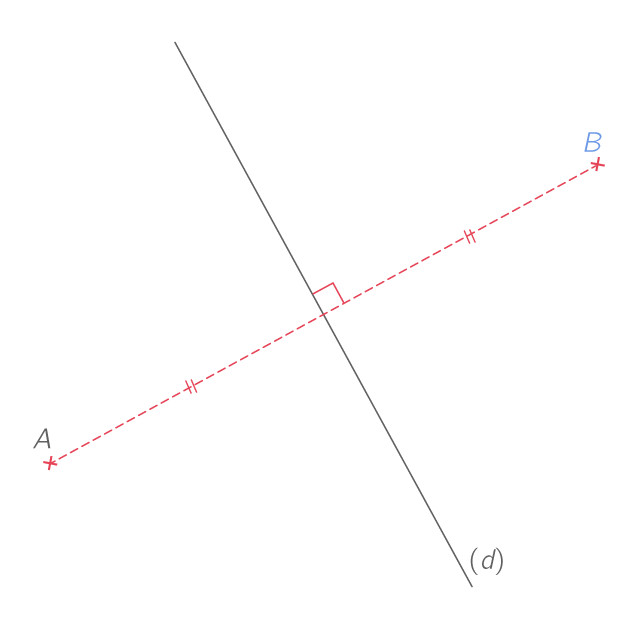
La médiatrice d'un segment est l'axe de symétrie de ce segment. Si \left( d \right) est la médiatrice du segment \left[ AB \right], on dit que le point B est le symétrique du point A par rapport à \left( d \right) (et inversement).
Le point B est le symétrique de A par rapport à la droite \left( d \right).
Inversement, le symétrique du point A par rapport à une droite \left( d \right) est le point B tel que \left( d \right) soit la médiatrice du segment \left[ AB \right]. Si le point A est sur la droite \left( d \right), son symétrique est lui-même : le point A est alors dit invariant.
Si un point est sur la médiatrice d'un segment, il est à égale distance des extrémités de ce segment.
Le point C appartient à la médiatrice \left( d \right) du segment \left[ AB \right]. Donc CA = CB.
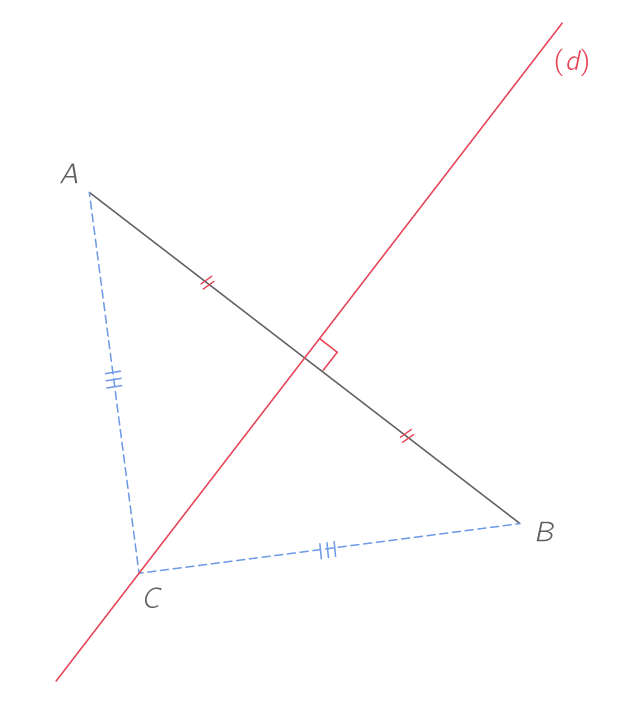
Inversement, si un point est à égale distance des extrémités d'un segment, il appartient à la médiatrice de ce segment.
On remarque que CA = CB. Le point C appartient donc à la médiatrice du segment \left[AB\right].
