Sommaire
1Justifier la dérivabilité de f 2Calculer la dérivée de f 3Étudier le signe de la dérivée de f 4Réciter le cours liant le signe de la dérivée aux variations de f 5Calculer les limites aux bornes et les extremums 6Dresser le tableau de variationsL'étude des variations de f, synthétisée dans son tableau de variations, est un élément incontournable d'une étude de fonction.
Dresser le tableau de variations de la fonction f définie sur \mathbb{R} par :
\forall x \in \mathbb{R}, f\left(x\right) =\dfrac{3x}{x^2+1}
Justifier la dérivabilité de f
On précise le domaine de dérivabilité de f.
La fonction f est dérivable sur \mathbb{R} en tant que quotient de fonctions dérivables sur \mathbb{R} dont le dénominateur ne s'annule pas sur \mathbb{R}.
Calculer la dérivée de f
On calcule la dérivée de f sur son ensemble de dérivabilité.
On remarque que f = \dfrac{u}{v} avec :
- \forall x \in \mathbb{R}, u\left(x\right) = 3x
- \forall x \in \mathbb{R}, v\left(x\right) = 1+x^2
On en déduit que :
f' = \dfrac{u'v-uv'}{v^2}
Avec :
- \forall x \in \mathbb{R}, u'\left(x\right) = 3
- \forall x \in \mathbb{R}, v'\left(x\right) = 2x
On en conclut que :
\forall x \in \mathbb{R}, f'\left(x\right) = \dfrac{3\left(x^2+1\right) -3x\times 2x}{\left(x^2+1\right)^2}
Donc :
\forall x \in \mathbb{R}, f'\left(x\right) = \dfrac{-3x^2+3}{\left(x^2+1\right)^2}
\forall x \in \mathbb{R}, f'\left(x\right) = \dfrac{-3\left(x^2-1\right)}{\left(x^2+1\right)^2}
\forall x \in \mathbb{R}, f'\left(x\right) = \dfrac{-3\left(x-1\right)\left(x+1\right)}{\left(x^2+1\right)^2}
Étudier le signe de la dérivée de f
On détermine le signe de f' sur son ensemble de dérivabilité.
On étudie le signe de chaque facteur.
- -3\lt0
- x-1\gt0\Leftrightarrow x\gt1
- x+1\gt0\Leftrightarrow x\gt-1
- \forall x \in \mathbb{R}, \left(x^2+1\right)^2 \gt 0
On obtient le tableau de signes suivant :
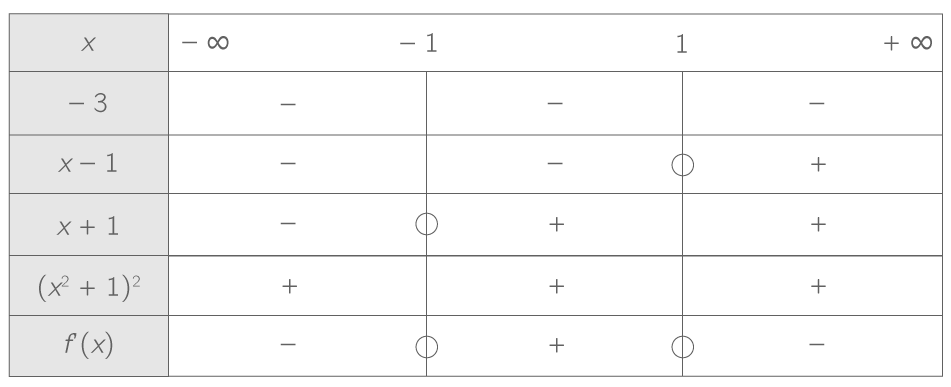
Réciter le cours liant le signe de la dérivée aux variations de f
On rappelle que :
- Si la fonction f' est positive sur un intervalle I, alors f est croissante sur I.
- Si la fonction f' est négative sur un intervalle I, alors f est décroissante sur I.
Il est vivement recommandé de noter explicitement ce théorème, considéré comme indispensable par la plupart des professeurs et correcteurs.
On sait que :
- Si la fonction f' est positive sur un intervalle I, alors f est croissante sur I.
- Si la fonction f' est négative sur un intervalle I, alors f est décroissante sur I.
Calculer les limites aux bornes et les extremums
On détermine les limites de f aux bornes de son ensemble de définition ainsi que la valeur de ses éventuels extremums locaux (qui sont atteints lorsque la dérivée s'annule et change de signe).
Pour calculer les limites de f en -\infty et +\infty on factorise numérateur et dénominateur par les termes de plus haut degré :
\forall x \in \mathbb{R}^*,f\left(x\right) = \dfrac{3x}{x^2\left(1+\dfrac{1}{x^2}\right)} = \dfrac{3}{x\left(1+\dfrac{1}{x^2}\right)}
On a :
\lim\limits_{x \to -\infty} \left(1+\dfrac{1}{x^2}\right) =\lim\limits_{x \to +\infty} \left(1+\dfrac{1}{x^2}\right) = 1
\lim\limits_{x \to +\infty} x=+\infty
\lim\limits_{x \to -\infty} x=-\infty
On en déduit par produit :
- \lim\limits_{x \to -\infty} x\left(1+\dfrac{1}{x^2}\right) =-\infty
- \lim\limits_{x \to +\infty} x\left(1+\dfrac{1}{x^2}\right) =+\infty
Donc, par quotient, on en conclut :
\lim\limits_{x \to -\infty} f\left(x\right)=\lim\limits_{x \to +\infty} f\left(x\right) = 0
On calcule ensuite les valeurs de f en -1 et en 1 :
- f\left(-1\right) = \dfrac{3\times \left(-1\right)}{1+\left(-1\right)^2}= -\dfrac{3}{2}
- f\left(1\right) = \dfrac{3\times 1}{1+1^2}= \dfrac{3}{2}
Dresser le tableau de variations
On synthétise dans le tableau de variations :
- Le domaine de définition de f, les valeurs où la dérivée change de signe et les éventuelles valeurs interdites
- Le signe de f'\left(x\right)
- Les variations de f
- Les limites et les extremums
On dresse enfin le tableau de variations complet de f :
