Sommaire
1Réciter le cours 2Déterminer graphiquement le sens de variation de f 3Donner le signe de f'\left(x\right) suivant les valeurs de xLa représentation graphique d'une fonction f permet d'obtenir, grâce à ses variations, le signe de sa dérivée f'.
On considère une fonction f définie sur \left[ -5;5 \right] dont la courbe représentative est donnée ci-dessous :
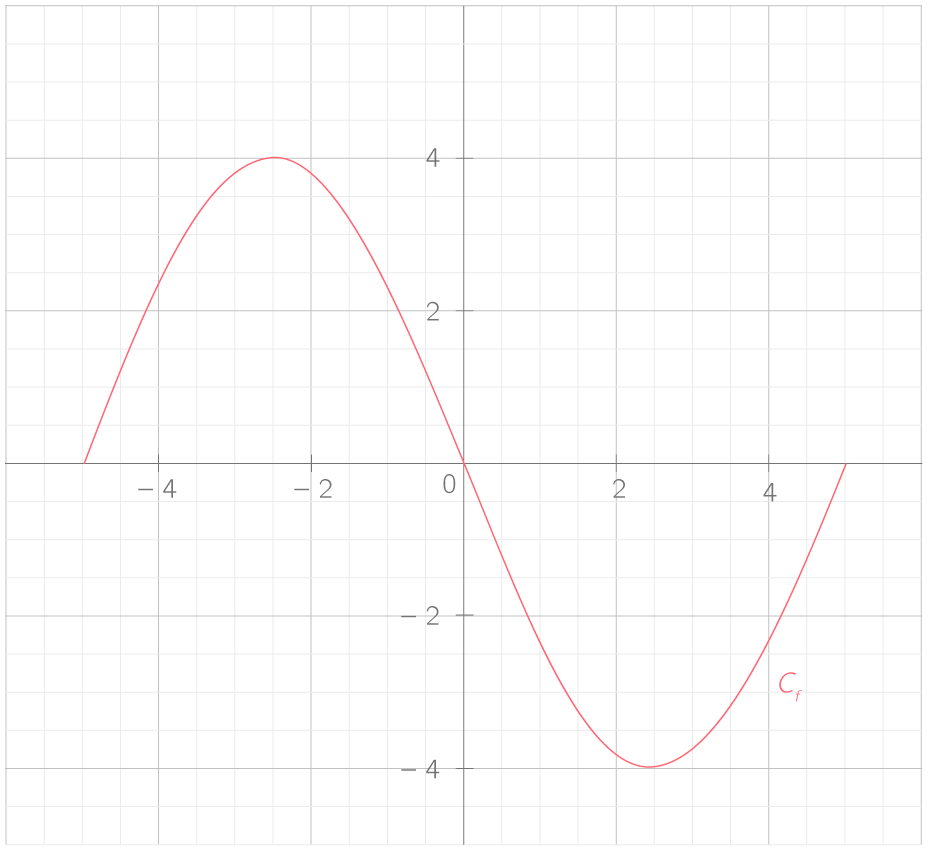
Déterminer le signe de la dérivée f' de la fonction f sur \left[ -5;5 \right].
Réciter le cours
On rappelle que :
- Si la fonction f est croissante sur un intervalle I, alors sa dérivée f' est positive sur I.
- Si la fonction f est décroissante sur un intervalle I, alors sa dérivée f' est négative sur I.
On sait que :
- Si la fonction f est croissante sur un intervalle I, alors sa dérivée f' est positive sur I.
- Si la fonction f est décroissante sur un intervalle I, alors sa dérivée f' est négative sur I.
Déterminer graphiquement le sens de variation de f
On identifie les extremums locaux sur le graphique. On détermine graphiquement, selon les valeurs de x, le sens de variation de la fonction f.
On identifie les extremums locaux sur le graphique :

On en déduit que :
- f est croissante sur \left[ -5;-2{,}5 \right] et sur \left[2{,}5;5 \right].
- f est décroissante sur \left[-2{,}5;2{,}5 \right].
Donner le signe de f'\left(x\right) suivant les valeurs de x
On peut alors en déduire le signe de f'\left(x\right) selon les valeurs de x, et éventuellement résumer le résultat dans un tableau de signes.
On en déduit que :
- f'\left(x\right) \gt 0 sur \left[ -5;-2{,}5 \right[ \cup \left]2{,}5;5 \right]
- f'\left(x\right) \lt 0 sur \left]-2{,}5;2{,}5 \right[
- f'\left(x\right) s'annule en -2,5 et 2,5
On peut résumer le résultat dans un tableau de signes :
