Sommaire
IEffets d'un déplacement, d'un agrandissement, d'une réduction sur une longueurIIEffet d'un déplacement, d'un agrandissement, d'une réduction sur une mesure d'angleIIIEffet d'un déplacement, d'un agrandissement, d'une réduction sur une aireIVEffet d'un déplacement, d'un agrandissement, d'une réduction sur un volumeAgrandissement et réduction d'une figure
Agrandir ou réduire une figure, c'est construire une figure de "même forme" en multipliant les longueurs de la figure initiale par un nombre k strictement positif.
- Si 0\lt k \lt 1, on parle d'une réduction.
- Si k=1, on parle d'une reproduction.
- Si k\gt1, on parle d'un agrandissement.
- Une homothétie de rapport k\gt1 est un agrandissement.
- Une homothétie de rapport 0\lt k \lt1 est une réduction.
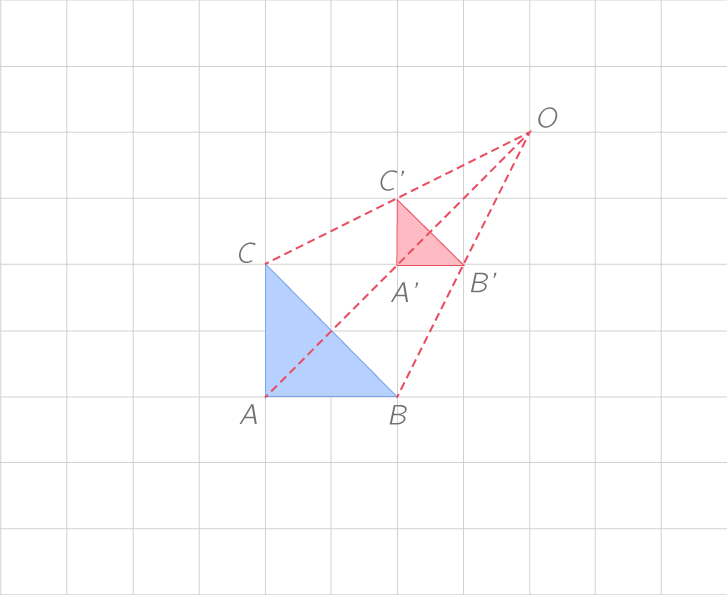
A'B'C' est l'image de ABC par l'homothétie de rapport 0,5.
Effets d'un déplacement, d'un agrandissement, d'une réduction sur une longueur
La symétrie axiale, la symétrie centrale, la translation et la rotation conservent les longueurs. Autrement dit, les longueurs de la figure image sont les mêmes que les longueurs de la figure initiale.
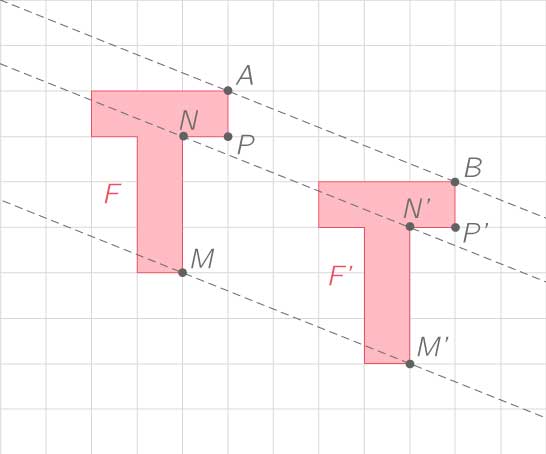
La figure F' est l'image de la figure F par la translation qui transforme A en B. On a donc par exemple :
- AP=BP'
- NP=N'P'
- NM=N'M'
Dans un agrandissement ou une réduction de rapport k, les longueurs sont multipliées par k.
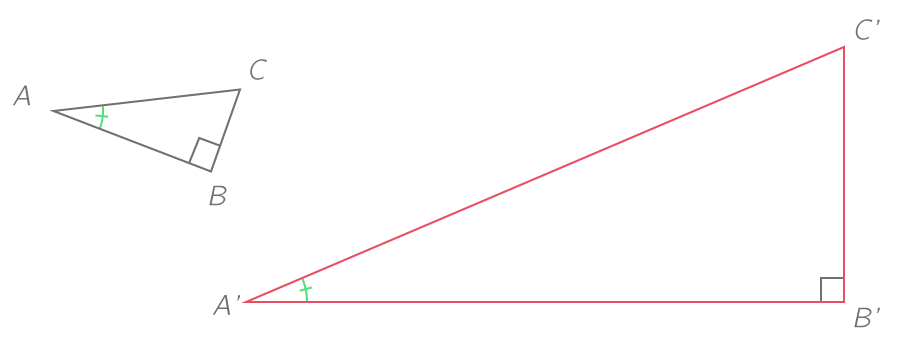
La figure rouge est un agrandissement de la figure noire de rapport 3. On a donc :
- A'B'=3\times AB
- A'C'=3\times AC
- C'B'=3\times CB
Effet d'un déplacement, d'un agrandissement, d'une réduction sur une mesure d'angle
La symétrie axiale, la symétrie centrale, la translation et la rotation conservent les mesures d'angles. Autrement dit, les mesures d'angles de la figure image sont les mêmes que les mesures d'angles de la figure initiale.

Le triangle A'B'C' est le symétrique du triangle ABC par rapport au point O. On a donc :
- \widehat{A'B'C'}=\widehat{ABC}
- \widehat{A'C'B'}=\widehat{ACB}
Dans un agrandissement ou une réduction de rapport k, les mesures d'angles sont conservées.
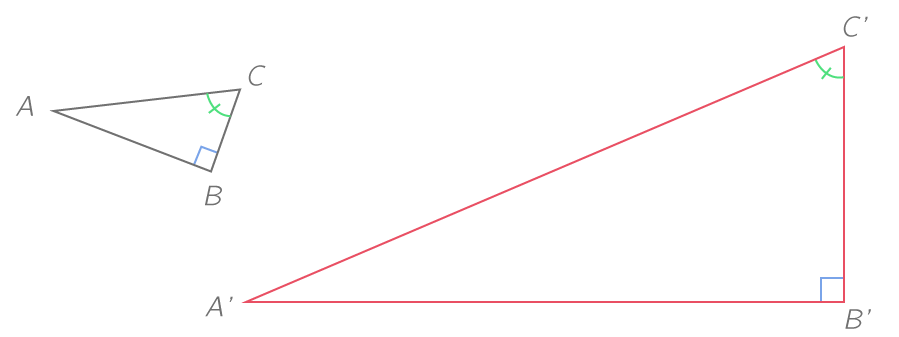
La figure rouge est un agrandissement de la figure noire de rapport 3. On a donc, par exemple :
- \widehat{A'B'C'}=\widehat{ABC}
- \widehat{A'C'B'}=\widehat{ACB}
Effet d'un déplacement, d'un agrandissement, d'une réduction sur une aire
La symétrie axiale, la symétrie centrale, la translation et la rotation conservent les aires. Autrement dit, l'aire de la figure image est la même que l'aire de la figure initiale.

Le triangle A'B'C' est l'image du triangle ABC par la rotation de centre O, d'angle 60° dans le sens anti-horaire. On a donc :
A_{A'B'C'}=A_{ABC}
Dans un agrandissement ou une réduction de rapport k, les aires sont multipliées par k^2.

La figure rouge est un agrandissement de la figure noire de rapport 3. On a donc :
A_{A'B'C'}=3^2\times A_{ABC}=9\times A_{ABC}
Effet d'un déplacement, d'un agrandissement, d'une réduction sur un volume
La symétrie axiale, la symétrie centrale, la translation et la rotation conservent les volumes. Autrement dit, si on applique l'une de ces transformations à un solide de l'espace, le volume du solide image est le même que le volume du solide initial.

La pyramide A'B'C'D' est l'image de la pyramide ABCD par la translation qui transforme A en A'. On a donc :
V_{A'B'C'D'}=V_{ABCD}
Dans un agrandissement ou une réduction de rapport k, les volumes sont multipliés par k^3.

La pyramide A'B'C'D' est un agrandissement de la pyramide ABCD de rapport 2. On a donc :
V_{A'B'C'D'}=2^3\times V_{ABCD}=8\times V_{ABCD}