Sommaire
ICosinus, sinus et tangente d'un angle aiguALe cosinusBLe sinusCLa tangenteDDéterminer un angle avec la calculatriceIIRelations trigonométriques fondamentalesCosinus, sinus et tangente d'un angle aigu
Le cosinus
Cosinus
Dans un triangle rectangle, le cosinus d'un angle aigu est égal à :
\cos\left(\alpha \right) =\dfrac{\textcolor{Blue}{\text{côté adjacent}}}{\textcolor{Red}{\text{hypoténuse}}}

Dans le triangle ABC rectangle en A, on a :
\cos\left( \widehat{ABC} \right) = \dfrac{AB}{BC} = \dfrac{6}{10} = \dfrac{3}{5}
\cos\left( \widehat{ACB} \right) = \dfrac{AC}{BC} = \dfrac{8}{10} = \dfrac{4}{5}
Le cosinus d'un angle aigu est toujours compris entre 0 et 1.
Le sinus
Sinus
Dans un triangle rectangle, le sinus d'un angle aigu est égal à :
\sin\left(\alpha \right) =\dfrac{\textcolor{Blue}{\text{côté opposé}}}{\textcolor{Red}{\text{hypoténuse}}}


Dans le triangle ABC rectangle en A, on a :
\sin\left( \widehat{ABC} \right) = \dfrac{AC}{BC} = \dfrac{8}{10} = \dfrac{4}{5}
\sin\left( \widehat{ACB} \right) = \dfrac{AB}{BC} = \dfrac{6}{10} = \dfrac{3}{5}
Le sinus d'un angle aigu est toujours compris entre 0 et 1.
La tangente
Tangente
Dans un triangle rectangle, la tangente d'un angle aigu est égal à :
\tan\left(\alpha \right) =\dfrac{\textcolor{Red}{\text{côté opposé}}}{\textcolor{Blue}{\text{côté adjacent}}}


Dans le triangle ABC rectangle en A, on a :
\tan\left( \widehat{ABC} \right) = \dfrac{AC}{AB} = \dfrac{8}{6} = \dfrac{4}{3}
\tan\left( \widehat{ACB} \right) = \dfrac{AB}{AC} = \dfrac{6}{8} = \dfrac{3}{4}
La tangente d'un angle aigu est toujours supérieure à 0, mais pas nécessairement inférieure à 1 comme le sinus et le cosinus.
Déterminer un angle avec la calculatrice
Déterminer un angle
Connaissant le cosinus, le sinus, ou la tangente d'un angle aigu, on peut retrouver la valeur de cet angle à l'aide des fonctions \cos^{-1}, \sin^{-1} et \tan^{-1} de la calculatrice.
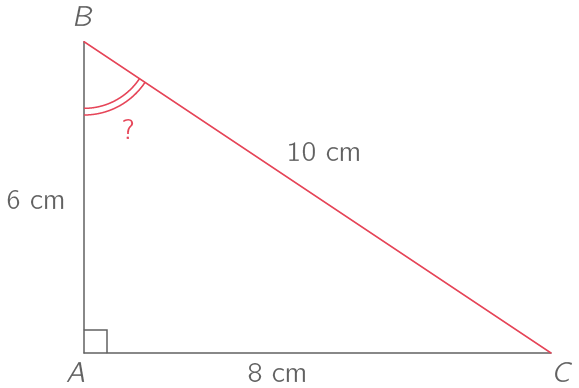
Dans le triangle ABC rectangle en A, on a :
\sin\left( \widehat{ABC} \right) = \dfrac{AC}{BC} = \dfrac{8}{10} = \dfrac{4}{5} d'où \widehat{ABC}=\sin^{-1}\left( \dfrac45 \right)\approx53^\circ.
Veiller à ce que la calculatrice soit réglée en degrés décimaux.
Relations trigonométriques fondamentales
Somme des carrés
Pour tout angle aigu \alpha :
\cos^{2}\left(\alpha \right) + \sin^{2}\left(\alpha \right) = 1
En connaissant par exemple le cosinus d'un angle, on peut en déduire le sinus.
Si \cos\left(\alpha\right)=\dfrac34 alors on peut écrire :
\left( \dfrac34 \right)^{2}+\sin^2\left( \alpha \right)=1
D'où :
\sin^2\left( \alpha \right)=1-\left( \dfrac34 \right)^{2}=1-\dfrac{9}{16}=\dfrac{7}{16}
Ainsi :
\sin\left(\alpha\right)=\sqrt{\dfrac{7}{16}}=\dfrac{\sqrt7}{4}
Tangente
Pour tout angle aigu \alpha différent de 90° :
\tan\left(\alpha \right) =\dfrac{\sin\left(\alpha \right)}{\cos\left(\alpha \right)}
En connaissant le sinus et le cosinus d'un angle on peut calculer sa tangente.
Si \sin\left(\alpha\right)=\dfrac12 et \cos\left(\alpha\right)=\dfrac{\sqrt3}{2}, alors :
\tan\left(\alpha\right)=\dfrac{\dfrac12}{\dfrac{\sqrt3}{2}}=\dfrac12\times\dfrac{2}{\sqrt3}=\dfrac{1}{\sqrt3}=\dfrac{\sqrt3}{3}