Quelle proposition correspond à la construction du segment \left[ CD \right], symétrique du segment \left[ AB \right] par rapport à la droite \left( d \right) représentés ci-dessous ?

Le symétrique d'un segment par rapport à une droite est un segment de même longueur.
Tracer les droites perpendiculaires à d
Tout d'abord, on trace deux droites perpendiculaires à la droite (d) passant respectivement par les points A et B.

Placer les points symétriques
On place ensuite les points C (symétrique du point A) et D (symétrique du point B) sur les deux droites perpendiculaires que l'on a tracées, de telle manière à ce que la droite (d) passe par le milieu des segments \left[ AC \right] et \left[ BD \right].
Pour cette étape, on peut utiliser une règle graduée ou un compas.

Tracer le segment symétrique
On trace le segment \left[ CD \right], symétrique du segment \left[ AB \right] par rapport à la droite (d).

Quelle proposition correspond à la construction du segment \left[ CD \right], symétrique du segment \left[ AB \right] par rapport à la droite \left( d \right) représentés ci-dessous ?

Le symétrique d'un segment par rapport à une droite est un segment de même longueur.
Tracer les droites perpendiculaires à d
Tout d'abord, on trace deux droites perpendiculaires à la droite (d) passant respectivement par les points A et B.

Placer les points symétriques
On place ensuite les points C (symétrique du point A) et D (symétrique du point B) sur les deux droites perpendiculaires que l'on a tracées, de telle manière à ce que la droite (d) passe par le milieu des segments \left[ AC \right] et \left[ BD \right].
Pour cette étape, on peut utiliser une règle graduée ou un compas.

Tracer le segment symétrique
On trace le segment \left[ CD \right], symétrique du segment \left[ AB \right] par rapport à la droite (d).

Quelle proposition correspond à la construction du segment \left[ CD \right], symétrique du segment \left[ AB \right] par rapport à la droite \left( d \right) représentés ci-dessous ?

Le symétrique d'un segment par rapport à une droite est un segment de même longueur.
Tracer les droites perpendiculaires à d
Tout d'abord, on trace deux droites perpendiculaires à la droite (d) passant respectivement par les points A et B.
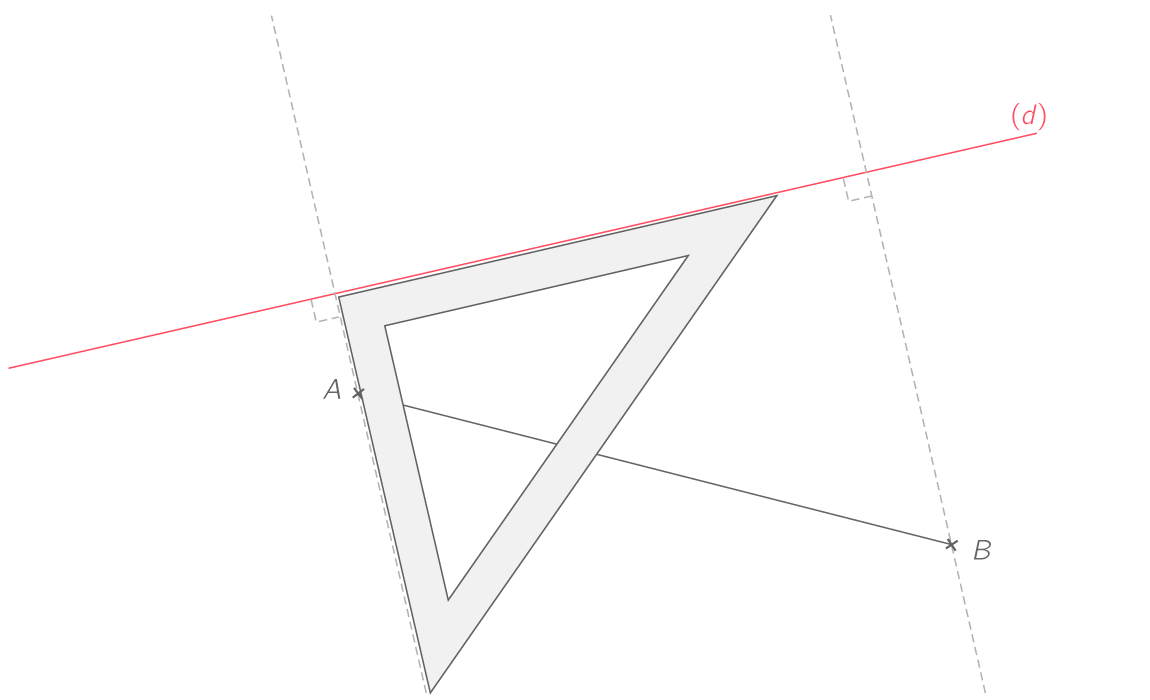
Tracer les droites perpendiculaires à d
Tout d'abord, on trace deux droites perpendiculaires à la droite (d) passant respectivement par les points A et B.

Placer les points symétriques
On place ensuite les points C (symétrique du point A) et D (symétrique du point B) sur les deux droites perpendiculaires que l'on a tracées, de telle manière à ce que la droite (d) passe par le milieu des segments \left[ AC \right] et \left[ BD \right].
Pour cette étape, on peut utiliser une règle graduée ou un compas.

Tracer le segment symétrique
On trace le segment \left[ CD \right], symétrique du segment \left[ AB \right] par rapport à la droite (d).

Quelle proposition correspond à la construction du segment \left[ CD \right], symétrique du segment \left[ AB \right] par rapport à la droite \left( d \right) représentés ci-dessous ?

Le symétrique d'un segment par rapport à une droite est un segment de même longueur.
Tracer les droites perpendiculaires à d
Tout d'abord, on trace deux droites perpendiculaires à la droite (d) passant respectivement par les points A et B.

Placer les points symétriques
On place ensuite les points C (symétrique du point A) et D (symétrique du point B) sur les deux droites perpendiculaires que l'on a tracées, de telle manière à ce que la droite (d) passe par le milieu des segments \left[ AC \right] et \left[ BD \right].
Pour cette étape, on peut utiliser une règle graduée ou un compas.

Tracer le segment symétrique
On trace le segment \left[ CD \right], symétrique du segment \left[ AB \right] par rapport à la droite (d).

Quelle proposition correspond à la construction du segment \left[ CD \right], symétrique du segment \left[ AB \right] par rapport à la droite \left( d \right) représentés ci-dessous ?

Le symétrique d'un segment par rapport à une droite est un segment de même longueur.
Tracer les droites perpendiculaires à d
Tout d'abord, on trace deux droites perpendiculaires à la droite (d) passant respectivement par les points A et B.

Placer les points symétriques
On place ensuite les points C (symétrique du point A) et D (symétrique du point B) sur les deux droites perpendiculaires que l'on a tracées, de telle manière à ce que la droite (d) passe par le milieu des segments \left[ AC \right] et \left[ BD \right].
Pour cette étape, on peut utiliser une règle graduée ou un compas.

Tracer le segment symétrique
On trace le segment \left[ CD \right], symétrique du segment \left[ AB \right] par rapport à la droite (d).
