Vocabulaire
Expérience aléatoire
Une expérience est dite aléatoire lorsque son résultat est lié au hasard et ne peut donc pas être prédit à l'avance avec certitude.
Le lancer d'un dé équilibré à 6 faces constitue une expérience aléatoire : il existe 6 résultats possibles, dont aucun n'est prévisible de façon certaine.
Éventualité (ou issue)
Les résultats possibles d'une expérience sont généralement appelés éventualités (ou issues).
Les éventualités de l'expérience aléatoire consistant à lancer un dé à 6 faces, notées e_i, sont :
- e_1 : face 1
- e_2 : face 2
- e_3 : face 3
- e_4 : face 4
- e_5 : face 5
- e_6 : face 6
Épreuve
On appelle épreuve une expérience dont les différentes issues sont aléatoires et auxquelles on peut attacher des fréquences d'apparition connues ou estimées.
Le lancer d'un dé équilibré à 6 faces constitue une épreuve. On sait que la fréquence d'apparition de chaque face est égale à \dfrac{1}{6}.
Événement
Un événement est un ensemble d'éventualités (ou d'issues).
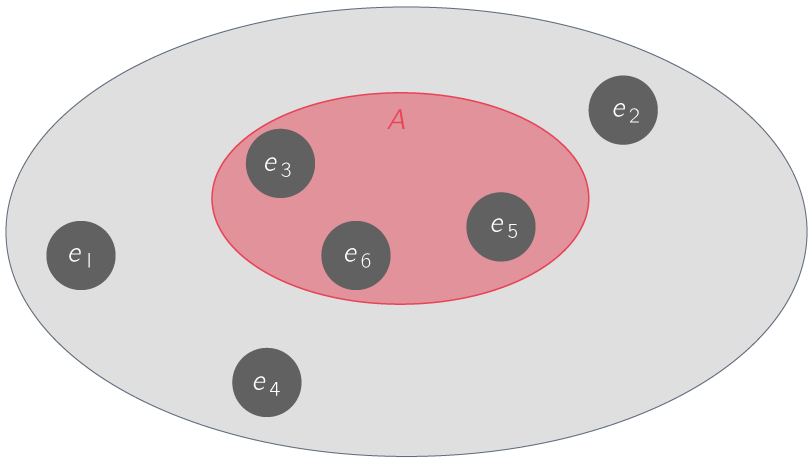
On considère le lancer d'un dé équilibré à 6 faces. On souhaite étudier l'événement A : "obtenir un multiple de 3 ou de 5".
Les éventualités correspondant à cet événement sont :
- e_3 : face 3
- e_5 : face 5
- e_6 : face 6
Événement élémentaire
Un événement ne contenant qu'une issue (ou éventualité) est dit élémentaire.
On considère le lancer d'un dé équilibré à 6 faces. On souhaite étudier l'événement A : "obtenir un multiple de 5".
Cet événement ne comportant qu'une issue, c'est un événement élémentaire.
Événements incompatibles
Deux événements sont dits incompatibles s'ils ne peuvent pas se produire simultanément.
On lance un dé à six faces. Soient les événements suivants :
- P : "obtenir un nombre pair "
- T : "obtenir 3"
Les événements P et T sont incompatibles : ils ne peuvent pas se réaliser en même temps.
Événement contraire
On appelle événement contraire de l'événement A, noté \overline{A}, l'ensemble des éventualités qui ne sont pas dans A.
On considère le lancer d'un dé équilibré à six faces. Soit :
M : "obtenir un multiple de 3" ce qui revient à "obtenir la face 3 ou la face 6".
L'événement contraire de M est :
\overline{M} : "ne pas obtenir un multiple de 3" ce qui revient à "n'obtenir ni la face 3 ni la face 6".
Cas d'équiprobabilité
Probabilité
Lorsque l'on effectue un très grand nombre de fois une expérience aléatoire de façon indépendante et dans les mêmes conditions, la fréquence de réalisation d'un événement E se rapproche d'un nombre que l'on appelle probabilité de cet événement. On la note p\left(E\right).
La probabilité d'un événement est un nombre compris entre 0 et 1. Elle exprime la "chance" qu'a cet événement de se produire (on dit aussi d'être réalisé).
On peut l'exprimer sous forme d'un nombre à virgule, d'une fraction ou d'un pourcentage.
Situation équiprobable
On appelle situation équiprobable une expérience où tous les événements élémentaires ont la même probabilité d'être réalisés.
Si on lance un dé équilibré, la probabilité de sortie de chaque face est égale. On est donc dans une situation d'équiprobabilité.
En situation d'équiprobabilité, la probabilité d'un événement A, notée p\left(A\right), est égale à :
\dfrac{\text{Nombre d'éventualités réalisant A}}{\text{Nombre total d'éventualités}}
On lance un dé équilibré à 6 faces. On cherche la probabilité de l'événement suivant :
A : "obtenir un multiple de 3 ou de 5"
Il existe 3 éventualités réalisant cet événement :
- e_3 : face 3
- e_5 : face 5
- e_6 : face 6
De plus, le dé étant équilibré, la situation est équiprobable et chaque face a 1 chance sur 6 de sortir. On en conclut finalement que la probabilité de l'événement A est égale à :
p\left(A\right)=\dfrac{3}{6}=0{,}5
Simulation
En utilisant sa calculatrice ou un tableur, on peut souvent simuler une expérience aléatoire de façon relativement simple.
Sur une calculatrice de la marque Texas Instruments, l'instruction " randn \left(1;6\right) " permet d'obtenir un nombre entier aléatoire entre 1 et 6. On trouve cette instruction en appuyant sur la touche " math ".
Sur une calculatrice de la marque Casio, l'instruction " \text{RandInt#} \left(1;6\right) " permet d'obtenir un nombre entier aléatoire entre 1 et 6. On trouve cette instruction en appuyant sur " ALPHA " et ",".
Pour simuler, à l'aide d'un tableur, 30 lancers d'un dé cubique équilibré dont les faces sont numérotées de 1 à 6 on peut procéder comme suit :
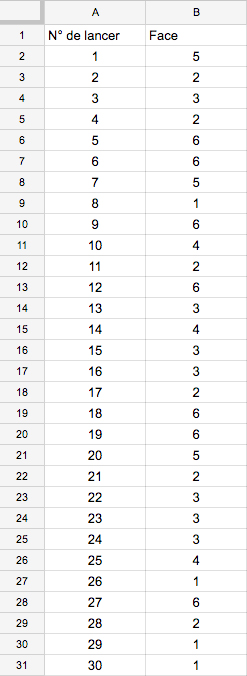
- Dans la cellule B2, on entre la formule " =ALEA.ENTRE.BORNES\left(1;6\right) " que l'on étire ensuite jusqu'à la cellule B31.
- On obtient une simulation de 30 lancers d'un dé équilibré dans la colonne B.
Même si l'expérience aléatoire possède des issues non numériques, on peut utiliser ces instructions pour simuler l'expérience.
Pour simuler, à l'aide d'un tableur, 25 lancers d'une pièce de monnaie, on peut procéder comme suit :
- On peut demander des nombres entiers aléatoires entre 0 et 1 et considérer que 0 correspond à "PILE" et 1 à "FACE".
- Alors la formule =SI\left(ALEA.ENTRE.BORNES\left(0;1\right)=0;"PILE";"FACE"\right) entrée dans la cellule B2 puis étirée jusqu'à la cellule B26 donne le résultat escompté.
Voici un exemple de ce que l'on peut obtenir :
