Sommaire
ILa symétrie centraleASymétrique d'un point, d'une figureBLes propriétés de la symétrie centraleIILe centre de symétrie d'une figureIIIComparaison des propriétés de la symétrie axiale et de la symétrie centraleIVAxes et centres de symétrie de figures usuellesVCaractérisation de la médiatriceLa symétrie centrale
Symétrique d'un point, d'une figure
Figures symétriques
Deux figures sont symétriques par rapport à un point O lorsqu'elles se superposent après avoir effectué un demi-tour autour du point O. Le point O est appelé « centre de symétrie ».

Symétrique d'un point
Deux points A et A' sont dits symétriques par rapport à un point O lorsque le point O est le milieu du segment \left[ AA' \right].
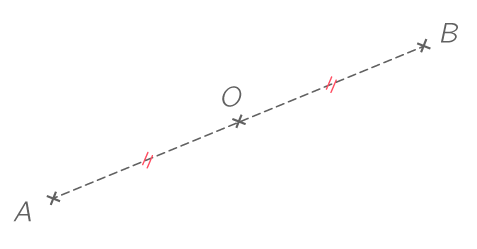
Le point B est le symétrique du point A par rapport à O. Inversement, le point A est le symétrique du point B par rapport à O.
On dit aussi que le point A' est le symétrique du point A par la symétrie de centre O.
Les propriétés de la symétrie centrale
- Le symétrique d'une droite par symétrie centrale est une droite parallèle.
- Le symétrique d'un segment par symétrie centrale est un segment de même longueur.
- Le symétrique d'un angle par symétrie centrale est un angle de même mesure.
- Plus généralement, le symétrique d'une figure par symétrie centrale est une figure superposable.

- Les droites \left( d \right) et \left( d' \right) sont parallèles.
- Les segments \left[ AB \right] et \left[ A'B' \right] ont la même longueur.
La symétrie centrale modifie toutefois le sens des figures (elle les « retourne » horizontalement et verticalement).

Les figures ABCDE et VWXYZ sont symétriques par rapport à O.
Le centre de symétrie d'une figure
Centre de symétrie
Une figure possède un centre de symétrie si son symétrique par rapport à ce centre est la figure elle-même.
Le point O est le centre de symétrie de la figure ci-dessous.
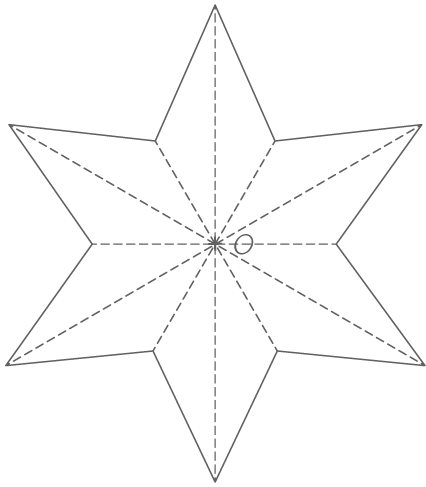

Le panneau de signalisation de fin de stationnement interdit admet un centre de symétrie.

Le panneau de signalisation d'un rond-point n'a pas de centre de symétrie.
Comparaison des propriétés de la symétrie axiale et de la symétrie centrale

Axes et centres de symétrie de figures usuelles

Caractérisation de la médiatrice
Médiatrice d'un segment
La médiatrice d'un segment est la droite qui coupe ce segment perpendiculairement, en son milieu.
Dans la figure ci-dessous, \Delta est la médiatrice du segment \left[AB \right].

Si un point M appartient à la médiatrice d'un segment \left[ AB \right], alors il est équidistant (à la même distance) de A et de B.
Autrement dit, si M appartient à la médiatrice d'un segment \left[ AB \right], alors MA=MB.

Réciproquement, si un point M est équidistant des deux extrémités d'un segment \left[ AB \right], alors M appartient à la médiatrice du segment \left[ AB \right].
Autrement dit, si MA=MB, alors M appartient à la médiatrice du segment \left[ AB \right].