Sommaire
Méthode 1A l'aide du taux d'accroissement 1Calculer le taux d'accroissement de f en a 2Déterminer la limite du taux d'accroissement 3ConclureMéthode 2Graphiquement 1Rappeler le cours 2Identifier la tangente à C_f au point d'abscisse a 3Calculer le coefficient directeur de la tangente 4ConclureMéthode 3Si l'on connaît la fonction dérivée de f 1Rappeler l'expression de f'\left(x\right) 2Calculer f'\left(a\right)A l'aide du taux d'accroissement
Une fonction f est dérivable en un réel a si et seulement si son taux d'accroissement en a admet une limite finie l lorsque h tend vers 0. Dans ce cas, f'\left(a\right)=l.
On considère la fonction f qui à tout réel x associe f\left(x\right) = x^2-x+1.
Montrer que f est dérivable en 1 et calculer f'\left(1\right).
Calculer le taux d'accroissement de f en a
Soit I un intervalle inclus dans l'ensemble de définition de f. Soient a\in I et h\neq0 tel que \left(a+h\right)\in I.
On écrit le taux d'accroissement de f entre a et a+h.
Il est égal à :
\dfrac{f\left(a+h\right)-f\left(a\right)}{h}.
Le taux d'accroissement de f entre 1 et 1+h (avec h\neq0 ) vaut :
\dfrac{f\left(1+h\right)-f\left(1\right)}{h} = \dfrac{\left(1+h\right)^2-\left(1+h\right)+1 - \left(1-1+1\right)}{h}
Déterminer la limite du taux d'accroissement
On simplifie l'expression du taux d'accroissement au maximum.
En particulier, si possible, on factorise par h au numérateur afin de le simplifier avec le dénominateur.
On simplifie l'expression. Pour tout réel h non nul :
\dfrac{f\left(1+h\right)-f\left(1\right)}{h} = \dfrac{1+2h+h^2-1-h+1 -1}{h}
\dfrac{f\left(1+h\right)-f\left(1\right)}{h} = \dfrac{h^2+h}{h}
On factorise par h non nul :
\dfrac{f\left(1+h\right)-f\left(1\right)}{h} = \dfrac{h\left(h+1\right)}{h}
On simplifie par h au numérateur et au dénominateur. On obtient, pour tout réel h non nul :
\dfrac{f\left(1+h\right)-f\left(1\right)}{h} = h+1
Conclure
Deux cas se présentent :
- Il ne reste plus de puissance de h au dénominateur. On peut alors "remplacer" h par 0 et le résultat, noté \lim\limits_{h \to 0} \dfrac{f\left(a+h\right)-f\left(a\right)}{h}, est égal à f'\left(a\right).
- Il reste une puissance de h au dénominateur. On ne peut pas "remplacer" h par 0, f n'est pas dérivable en a.
Il n'y a pas de puissance de h au dénominateur. On peut donc "remplacer" h par 0. On obtient :
\lim\limits_{h \to 0} \dfrac{f\left(1+h\right)-f\left(1\right)}{h} = 1\in \mathbb{R}
Donc f est dérivable en 1 et f'\left(1\right) = 1 .
Graphiquement
f'\left(a\right) est le coefficient directeur de la tangente à la courbe représentative de f au point d'abscisse a.
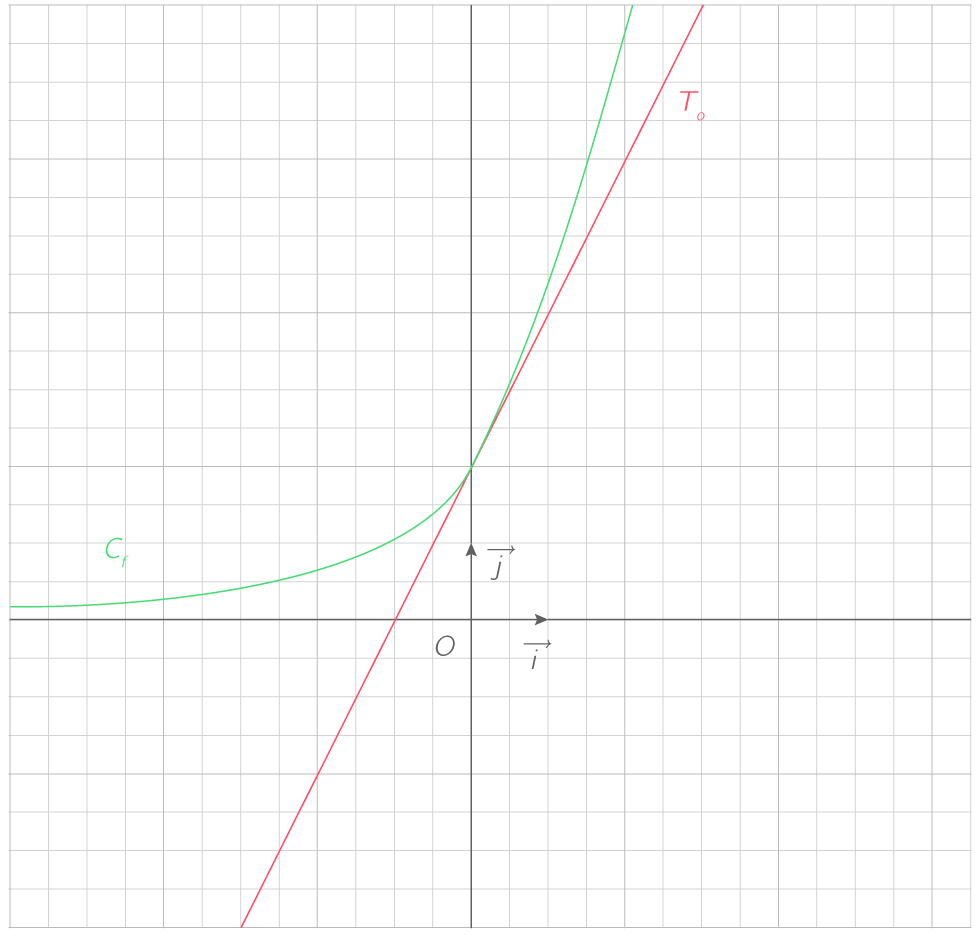
On considère la fonction f, dont la courbe représentative C_f est donnée ci-dessous. Déterminer graphiquement la valeur de f'\left(0\right).
Rappeler le cours
On rappelle que f'\left(a\right) est le coefficient directeur de la tangente à C_f au point d'abscisse a.
f'\left(0\right) est le coefficient directeur de la tangente à C_f au point d'abscisse 0.
Identifier la tangente à C_f au point d'abscisse a
On repère sur le graphique la tangente à Cf au point d'abscisse a.
T_0 est la tangente à C_f au point d'abscisse 0.
Calculer le coefficient directeur de la tangente
On calcule le coefficient directeur de cette tangente. Pour cela, on choisit deux points A\left(x_A;y_A\right) et B\left(x_B;y_B\right) appartenant à la tangente.
Le coefficient directeur vaut alors :
\dfrac{y_B-y_A}{x_B-x_A}
Si la tangente est horizontale, son coefficient directeur vaut 0.
A\left(-1;0\right) et B\left(2;6\right) appartiennent à T_0.

Donc le coefficient directeur de T_0 vaut :
\dfrac{y_B-y_A}{x_B-x_A} = \dfrac{6-0}{2-\left(-1\right)}
\dfrac{y_B-y_A}{x_B-x_A} = \dfrac{6}{3}
\dfrac{y_B-y_A}{x_B-x_A} = 2
Conclure
f'\left(a\right) est égal au coefficient directeur de la tangente à Cf au point d'abscisse a.
On conclut : f'\left(a\right) = \dfrac{y_B-y_A}{x_B-x_A}.
f'\left(0\right) est égal au coefficient directeur de la tangente à C_f au point d'abscisse 0.
Ainsi, f'\left(0\right) = 2.
Si l'on connaît la fonction dérivée de f
Si f est dérivable sur un intervalle I et que l'on connaît l'expression de f'(x) sur I, on peut alors calculer f'\left(a\right), avec a \in I.
On considère une fonction f définie sur \mathbb{R}. On donne \forall x \in\mathbb{R}, f'\left(x\right) = 4x-3. Déterminer la valeur de f'\left(2\right).
Rappeler l'expression de f'\left(x\right)
f' est l'expression de la dérivée de f, sur un intervalle I donné. On rappelle son expression.
On a :
\forall x \in \mathbb{R},f'\left(x\right) = 4x-3
Calculer f'\left(a\right)
On remplace x par a dans l'expression de f'\left(x\right). On obtient ainsi la valeur de f'\left(a\right).
On remplace x par 2 dans l'expression de f'. On obtient :
f'\left(2\right)= 4\times 2-3
Soit :
f'\left(2\right)= 5